Парадокс это мысль, которая противоречит сама себе, но и в одном и в другом случае является истиной. Логические размышления, которые будоражат умы всех мыслителей уже не один десяток лет. Представляем вам 10 парадоксов из нашей жизни:
Парадокс исчезающей клетки — известный класс задач (оптических иллюзий) на перестановку фигур, в которых изначально в условии введена замаскированная ошибка.
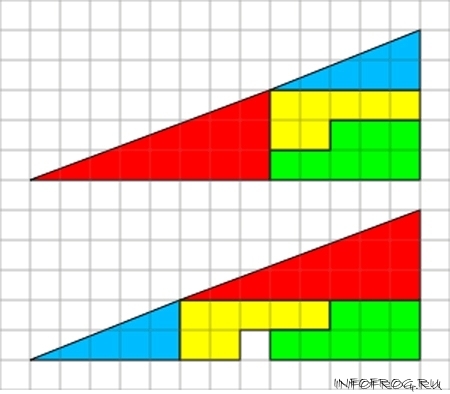
Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади (S13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это — вогнутый 4-угольник). Это отчётливо заметно на рисунках 2 и 3 — «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) — внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.
«Гипотенуза» на самом деле является ломаной линией
Парадокс курицы и яйца
Вопрос, который мучает уже не одно поколение — «Что было раньше, курица или яйцо?». С помощью этого вопроса древние философы искали путь, чтобы объяснить появление жизни на земле и всей вселенной в целом. Этот парадокс описывает явление круговой череды причины и следствия. Чтобы отложить яйцо, должна быть курица, но чтобы курица отложила яйцо, она должна была родиться , всё из того же яйца.
Парадокс дней рождения
Парадокс дней рождения — утверждение, гласящее, что если дана группа из 23 или более человек, то вероятность того, что хотя бы у двух из них дни рождения (число и месяц) совпадут, превышает 50 %. С практической точки зрения это означает, что если, например, в вашем классе более 22 учеников, то более вероятно, что у кого-то из одноклассников дни рождения придутся на один день, чем что у каждого будет свой собственный день рождения.
Для 60 и более человек вероятность такого совпадения превышает 99 %, хотя 100 % она достигает, согласно принципу Дирихле, только когда в группе не менее 367 человек (с учётом високосных лет).
Один из способов понять на интуитивном уровне, почему в группе из 23 человек вероятность совпадения дней рождения у двух человек столь высока, состоит в осознании следующего факта: поскольку рассматривается вероятность совпадения дней рождения у любых двух человек в группе, то эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Так как порядок людей в парах не имеет значения, то общее число таких пар равно числу сочетаний из 23 по 2, то есть (23 × 22)/2 = 253 пары. Посмотрев на это число, легко понять, что при рассмотрении 253 пар людей вероятность совпадения дней рождения хотя бы у одной пары будет достаточно высокой.
Ключевым моментом здесь является то, что утверждение парадокса дней рождения говорит именно о совпадении дней рождения у каких-либо двух членов группы. Одно из распространённых заблуждений состоит в том, что этот случай путают с другим — похожим, на первый взгляд, — случаем, когда из группы выбирается один человек и оценивается вероятность того, что у кого-либо из других членов группы день рождения совпадёт с днем рождения выбранного человека. В последнем случае вероятность совпадения значительно ниже.
Парадокс парикмахера (брадобрея): Если парикмахер бреет всех, кто не бреется сам, то кто бреет парикмахера?
Представьте, что вы проходите мимо парикмахерской с табличкой, на которой написано: «Ты бреетесь сами? Если нет, то и я побрею вас! Брею любого, кто не бреется сам, и никто другой кроме меня.» Всё вроде бы просто, пока в голове не возникает мысль — а кто же бреет парикмахера? Если он себя не бреет, то он относится к тем жителям деревни, которых он должен брить. Значит, он должен себя брить. Если же он себя бреет, то он не относится к тем жителям своей своей деревни, которых он должен брить. Значит, он не должен себя брить.
Этот парадокс пытался обойти ученый Бертран Рассел используя теорию множеств, ну или просто можно предположить, что парикмахер — женщина.
Парадокс Пиноккио: Что будет, если Пиноккио скажет: «Мой нос сейчас вырастет?»
Как известно, что у Пиноккио нос становился длиннее, если он врал, но что будет в той ситуации, если Пиноккио скажет: «Мой нос сейчас вырастет»? И любая попытка придать этому выражению статус лжи или истины приводит к бесконечному противоречию.
Парадокс бережливости: Чем больше мы откладываем на черный день, тем быстрее он наступит.
Парадокс формулируется следующим образом: «Чем больше мы откладываем на черный день, тем быстрее он наступит». Если во время экономического спада все начнут экономить, то совокупный спрос уменьшится, что повлечет за собой уменьшение зарплат и, как следствие, уменьшение сбережений. То есть можно утверждать, что когда все экономят, то это неизбежно должно привести к уменьшению совокупного спроса и замедлению экономического роста.
Проще говоря, если все люди, резко начнут экономить и откладывать деньги, то все окажутся в итоге бедными. Тем самым: чем больше у всех денег в заначке, тем все беднее. Соответственно, для экономического роста необходимо увеличивать совокупные расходы, которые будут заставлять расти совокупный доход, но это уже обратная модель, так как сбережений у людей просто не будет оставаться.
Парадокс Галилея: Хотя квадраты чисел состоят из натуральных чисел, квадратное число всё равно будет больше количества натуральных чисел.
Парадокс Галилея демонстрирует одно из удивительных свойств бесконечных множеств. В своей последней научной работе «Две науки» , Галилей сделал противоречивые заявления о натуральных числах. Квадратные числа состоят из натуральных чисел и при увеличении квадратных чисел, количество натуральных чисел тоже будет увеличиваться, а так как количество и тех и других чисел бесконечно, то по достижению бесконечности оба числа должны сравняться. Подробнее и понятнее это парадокс объясняется в видео ниже.
Парадокс Тесея : Если заменить все части корабля, будет ли это все тот же корабль?
Корабль Тесея, парадокс Тесея — парадокс, который можно сформулировать так: «Если все составные части исходного объекта были заменены, остаётся ли объект тем же объектом?».
Согласно греческому мифу, пересказанному Плутархом, корабль, на котором Тесей вернулся с Крита в Афины, хранился афинянами до эпохи Деметрия Фалерского, и ежегодно отправлялся со священным посольством на Делос. При починке в нём постепенно заменяли доски, до тех пор, пока среди философов не возник спор, тот ли это ещё корабль, или уже другой, новый? Кроме того, возникает вопрос: в случае постройки из старых досок второго корабля какой из них будет настоящим?
Аристотель утверждал, что это остается всё тот же корабль, так как его суть не изменилась. А другой мыслитель Терри Пратчетт, привел пример с топором, у которого в следствии износа, время от времени время меняется ручка, он утверждал, что этот топор уже не является всё тем же физически, но эмоционально это один и тот же топор.
Парадокс дедушки: Что будет, если бы вы смогли вернуться назад во времени и убить своего дедушку, прежде чем он встретит вашу бабушку?
Парадокс дедушки впервые был описан писателем-фантастом Рене Баржавелем в 1943 году в книге «Le Voyageur неблагоразумно» (Неосторожный путешественник). Парадокс заключается в следующем, что было бы, если бы человек , который мог бы путешествовать во времени, переместился в то время, когда его дедушка ещё не встретил его бабушку, и убил бы его. По логике он бы просто перестал не родился на свет, так как у его дедушки не было бы потомка в лице путешествующего, а если он не родился, то соответственно он не мог бы пропутешествовать во времени и убить своего дедушку, а следовательно он бы родился. Мыслители также предполагают, что убив своего дедушку, он бы просто может измениться сам и существовать в альтернативной реальности, так как его бабушка встретила бы другого мужчину и родила ребенка, и это был бы один и тот же путешественник, только уже с другими генами.
Парадокс ценностей: Почему бриллианты стоят дороже, чем вода, если вода жизненно необходима для человека, в то время как бриллианты для жизни бесполезны?
Парадокс ценностей, также известный как водно-алмазный парадокс, является очевидным противоречием, вода необходима для выживания, но бриллианты имеют гораздо более высокую цену на рынке. При низких уровнях потребления, вода гораздо ценнее, чем бриллианты. Дело в том, что доступной воды на данный момент больше чем бриллиантов, и не всё человечество остро нуждается в воде. Если оценивать полезность бриллианта, то стакан воды будет куда более полезен, чем драгоценный камень, но на рынке вам никто не продаст бриллиант по цене стакана воды.